研晟考研，专注清华北大等985/211名校考研辅导，拥有完善的服务团队，专属定制化的考研备考规划，力争实现每位学子的考研梦、名校梦。

 考试科目 601 数学分析   考试形式 笔试（闭卷）  考试时间 180 分钟  考试总分 150 分 

一、总体要求

主要考察学生对《数学分析》的基本知识、基本理论和基本技能的掌握情况以及利用数学分析 的理论与方法分析问题、解决问题的能力. 

二、内容

1. 集合与函数

1） 实数集 R ，有限集、可数集、不可数集，实数系的连续性，最大数与最小数，上、下确界， 确界存在性定理、单调有界性定理、闭区间套定理、Bolzano-Weierstrass 定理、Cauchy 收敛原理.

2）点集拓扑初步：度量空间、紧集、完全集、连通集、 R 2 上的距离、邻域、聚点、界点、边 界、开集、闭集、有界（无界）集、R n 上的闭矩形套定理、Heine-Borel 定理(有限覆盖定 理)以及上述概念和定理在 R n 上的推广.

3） 函数、映射、变换等概念及其几何意义，反函数与逆变换，反函数定理与隐函数定理，初 等函数以及与之相关的性质.

2. 极限与连续 

1） 数列极限、收敛数列的基本性质（极限唯一性、有界性、保号性、不等式性质）. 

2） 无穷大量、Stolz 定理、上（下）极限及其应用.

3) 数列收敛的条件（Cauchy 准则、单调有界原理、数列收敛与其子列收敛的关系）. 

3）一元函数极限的定义、函数极限的基本性质（唯一性、局部有界性、保号性、不等式性质）， Heine 归结原则和 Cauchy 收敛准则，两个重要极限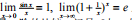  及其应用， 计算一元函数极限的各种方法，无穷小量与无穷大量、阶的比较，记号 O 与 o 的意义，多 元函数重极限与累次极限概念、基本性质，二元函数的二重极限与累次极限的关系. 

4） 函数连续与间断、一致连续性、连续函数的局部性质（局部有界性、保号性），有界闭集 上连续函数的性质（有界性、最大值最小值定理、介值定理、一致连续性）. 

3. 一元函数微分学 

1）导数及其几何意义、可导与连续的关系、导数的各种计算方法，微分及其几何意义、可微 与可导的关系、一阶微分形式不变性. 

2）微分学基本定理：Fermat 定理，Rolle 定理，Lagrange 定理，Cauchy 定理，Taylor 公式(Peano 余项、Lagrange 余项、Cauchy 余项). 

3）一元微分学的应用：函数单调性的判别、极值、最大值和最小值、凸函数及其应用、曲线 的凹凸性、拐点、渐近线、函数图象的讨论、洛必达（L'Hospital）法则、近似计算.

4. 多元函数微分学 

1） 偏导数、全微分及其几何意义，可微与偏导存在、连续之间的关系，复合函数的偏导数 与全微分，一阶微分形式不变性，方向导数与梯度，高阶偏导数，混合偏导数与顺序无 关性，二元函数中值定理与 Taylor 公式.

2） 隐函数存在定理、隐函数组存在定理、隐函数（组）求导方法、逆映射定理. 

3） 偏导数的几何应用（平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面 与法线）.

4） 极值问题（必要条件与充分条件），条件极值与 Lagrange 乘数法。

5. 一元函数积分学

1）原函数与不定积分、不定积分的基本计算方法（直接积分法、换元法、分部积分法）、有 理 函数积分：  R(cos x,sin x)dx 型，  R(x, ax 2  bx  c )dx 型.

2）定积分及其几何意义、可积条件（必要条件、充要条件： ixi   ）、可积函数类.

3）定积分的性质（关于区间可加性、不等式性质、绝对可积性、定积分第一中值定理）、变 上限积分函数、微积分基本定理、N-L 公式及定积分计算、定积分第二中值定理.

4）无限区间上的广义积分、Cauchy 收敛准则、绝对收敛与条件收敛、f (x) 非负时 ( ) a f x dx  的收敛性判别法（比较原则、柯西判别法）、一般函数反常积分的收敛判别法（Abel 判 别法 Dirichlet 判别法）、无界函数广义积分概念及其收敛性判别法.

5）微元法及其几何应用（平面图形面积、已知截面面积函数的体积、曲线弧长与弧微分、旋 转体体积）.

6. 多元函数积分学

1）二重积分及其几何意义、二重积分的计算（化为累次积分、极坐标变换、一般坐标变换）. 

2）三重积分、三重积分计算（化为累次积分、柱坐标、球坐标变换）. 

3）重积分的应用（体积、曲面面积、重心、转动惯量等）.

4）第一型曲线积分、曲面积分的概念、基本性质、计算.

5）第二型曲线积分概念、性质、计算；Green 公式，平面曲线积分与路径无关的条件.

6）曲面的侧、第二型曲面积分的概念、性质、计算，Gauss 公式、Stokes 公式，两类线积分、 两类面积分之间的关系.

7）含参变量的常义积分及其连续性、可微性、可积性，运算顺序的可交换性.含参变量广义 积分的一致收敛性及其判别法，含参量广义积分的连续性、可微性、可积性，运算顺序的 可交换性，Euler 积分、Beta 函数、Gamma 函数. 

7. 无穷级数

1）数项级数 数项级数及其敛散性，数项级数的和，Cauchy 准则，收敛的必要条件，收敛级数基本性质； 正项级数收敛的充分必要条件，比较原则、比式判别法、根式判别法以及它们的极限形式； 交错级数的 Leibniz 判别法；一般项级数的绝对收敛、条件收敛性、Abel 判别法、Dirichlet 判别法. 

2）函数项级数 函数列与函数项级数的一致收敛性、Cauchy 准则、一致收敛性判别法（M-判别法、Abel 判 别 法 、 Dirichlet 判 别 法 ） 、 一 致 收 敛 函 数 列 、 函 数 项 级 数 的 性 质 及 其 应 用 、 Stone-Weierstrass 逼近定理.

3）幂级数 幂级数概念、Abel 定理、收敛半径与区间，幂级数的一致收敛性，幂级数的逐项可积性、 可微性及其应用，幂级数的和函数的求法，函数的幂级数展开.

4）Fourier 级数 三角级数、三角函数系的正交性、2 及 2 l 周期函数的 Fourier 级数展开、 Beseel 不等式、 Riemanm-Lebesgue 定理、Fourier 级数的收敛性定理、Fourier 级数的性质、Fourier 变换 及其性质